| nessesary | ||
| classes_myproject.png | ||
| file_read_write.py | ||
| main.py | ||
| matrix.py | ||
| packages_myproject.png | ||
| README.md | ||
| testing.py | ||
Calculator for Matrix and Algebra
This is Text-based user interface program that use to solve matrix and algebra problems.
Table of Content
Overview
Calculator for Matrix and Algebra can solve some expression that not too complex such as expression that doesn't have much nested parentheses.
It can solve Single Variable Equation and can expand the polynomial.
Some function maybe buggy but If the expression is not contain math function or nested parentheses, It works at its finest.
Features
Calculator for Matrix and Algebra provide the following function.
- Ability to solve for basic quadratic function.
- Calculate operations of Polynomial function e.g. +/-/*/÷/^.
- Calculate operations of Matrix e.g. Inverse/Tranpose/Basic Operation/Determinant.
- Evaluate the expression(No Variable) that has complex parentheses.
- Evaluate the expression(with Variable) such as First degree equation, quadratic equation.
- Some basic algebra operation. e.g. Find reduce form of Fraction etc.
Requirement
This program has been created in Python 3.10.5 and has the following built-in module.
Program design
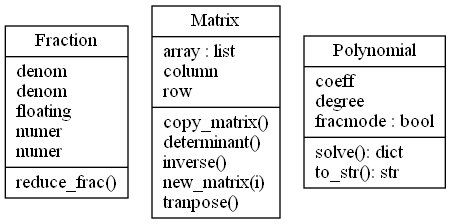
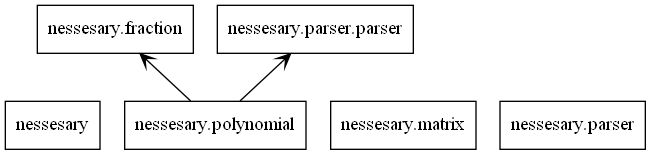
- This is UML Class Diagram of this program.
Code structure
- This file is the main file that read the input and return the result.
- Contains function that use to read and write json file.
- Implement Class Polynomial that contain function to solve, change between array and string form.
- Implement Class Matrix that contain function to find determiannt, inverse and Tranpose.
- Implement Class Fraction that contain function to turn float into fraction and can evaluate reduce form.
- Contain all parsing function such as function that parse string of polynomial to array list.
- process the string data inside the program. Use function in this file with polynomial.py to solve the single-variable equation.
Install and Usage
Clone this repository and run the main.py
$ git clone https://github.com/Sosokker/Calculator-for-Matrix-and-Algebra
Guide/Documentation
After the running of the main.py. You can type the command and input into the terminal that look like this.
[1] <- This is line-count.
There are two types of command, input style.
No need expression command and Need expression command.
Command or Command[expression]
Whitespace and Case are not matter. Command is same as command.
Syntax
| operator | meaning | |||
|---|---|---|---|---|
| + | add | |||
| - | substract | |||
| * or adjacant | multiply | |||
| / | Division | |||
| ^ | Power |
For example.
[1] history
# RESULT OF THE INPUT COMMAND
[2] det[[1,2],[3,4]]
# RESULT OF THE INPUT COMMAND
Every command you put in and result of it will be save in history.json file.
Equation
First order and Second order equation can be solved in this program. ⚠️ Other than these type of equaton can't be solved by now⚠️ Varible must be x ⚠️
-
solve[equation or expression] -> equation/expression str
- This Command use to solve First order and Second order equation and can use like poly[expression] (Next command in this guide).
=================================== [1]: solve[-3x^2+2x+1=2x^2-4x+1] Input: -3x^2+2x+1=2x^2-4x+1 =============================== Solution to -3x^2+2x+1=2x^2-4x+1 Answer #1: x = 1.2 | x = 6/5 Answer #2: x = -0.0 | x = 0 =============================== [2]: solve[-28x^2+0.5x-14.32x^2 = 10+5-4x^3] Input: -28x^2+0.5x-14.32x^2=10+5-4x^3 =============================================== Can't find solution to this expression.(Program can only find solution up too 2nd degree polynomial) [3]: solve[(2x-1)^2 = 0] Input: (2x-1)^2=0 ========================= Solution to (2x-1)^2=0 Answer #1: x = -0.5 | x = -1/2 ========================= -
sim or simplify[expression] -> equation/expression str
- This Command use to simplify First order and Second order equation into expanding form.
[1]: sim[(x-1)^2] Result of Simplify: x^2-2x^1+x^0 [2]: sim[x-x^2+5x-2x^2+(3x-2)^4] Result of Simplify: 81x^4-216x^3+216x^2-96x^1+16x^0
Polynomial
Polynomial in this class is store in form of array. This are the following command.
-
Polynomial or poly[expression] -> expression str or list
- This Command use to print all property of the polynomial that user input. (Answer will be given in both fraction and float form but if answer is complex number Its will be given in floating form only)
⚠️Warning⚠️ Can only solve first power equation, quadratic equation. If enter third, fourth,... degrees equation. Error will occur! ⚠️ (Sorry about this I'didn't implement it yet)
[1]: poly[3x^2-4x-10]
Input Polynoimial: 3x^2-4x-10
===============================
Solution to 3x^2-4x-10 = 0
Answer #1: x = -1.2769839649484336 | x = -798114978092771/625000000000000
Answer #2: x = 2.610317298281767 | x = 2610317298281767/1000000000000000
[2]: poly[x+31-x^2]
Input Polynoimial: x+31-x^2
=============================
Solution to x+31-x^2 = 0
Answer #1: x = 6.0901699437494745 | x = 12180339887498949/2000000000000000
Answer #2: x = -5.0901699437494745 | x = -10180339887498949/2000000000000000
===============================
Basic Operation
Evaluate operation of Matrix, Polynomial, algebra element.
-
evaluate[expression] -> expression: string(mathematic expression) e.g. evaluate[1+2(5)]
- Evaluate the operation of expression, Matrix, Polynomial.
[1]: evaluate[1+2(5)] Result: 11
Matrix
Matrix in this class store in form of nested list.
-
Matrix[expression] -> expression: nested list
- This Command use to print all property of the Matrix that user input.
[1]: Matrix[[1,2],[3,4]] Input Matrix: Matrix(([1, 2], [3, 4])) Determinant: -2 Tranpose Matrix: Matrix([[1, 3], [2, 4]]) Inverse Matrix: Matrix([[-2.0, 1.0], [1.5, -0.5]]) -
det[expression] -> expression: nested list
- This Command use to find determinant of matrix.
[1]: det[[1,2],[3,4]] Determinant: -2 -
tranpose[expression] -> expression: nested list
- This Command use to find tranpose of matrix.
[1]: tranpose[[1,2],[3,4]] Tranpose Matrix: Matrix([[1, 3], [2, 4]]) -
inverse[expression] -> expression: nested list
- This Command use to find inverse of matrix.
[1]: inverse[[1,2],[3,4]] Inverse Matrix: Matrix([[-2.0, 1.0], [1.5, -0.5]]) NOTE: inverse of matrix 3x3 4x4 ... is not the precise but 2x2 is precise.⚠️NOTE⚠️ Some inverse to nxn matrix when n >= 3 sometimes not that precise. I will try to fix it again.
Contributing
Pull requests are always welcome and that would be a honor. This first Python project I've dones. I practice using OOP and using github in this work so many parts of code look a bit messy. 🙈
Thank you so much.